前言

声明：参考来源互联网，有任何争议可以留言。站在前人的肩上，我们才能看的更远。

本教程纯手打，致力于最实用教程，不需要什么奖励，只希望多多转发支持。 欢迎来我公众号，希望可以结识你，也可以催更，微信搜索：JavaPub

有任何问题都可以来谈谈 ！

堆排序在常用排序算法中属于比较难理解的，本篇就以最简单的方式讲解。如果还有什么疑问，

1.什么是堆？

• 弄清楚**以前，我们先要知道什么是**？

堆是具有以下性质的完全二叉树：每个结点的值都大于或等于其左右孩子结点的值，称为大顶堆；或者每个结点的值都小于或等于其左右孩子结点的值，称为小顶堆。

下图：

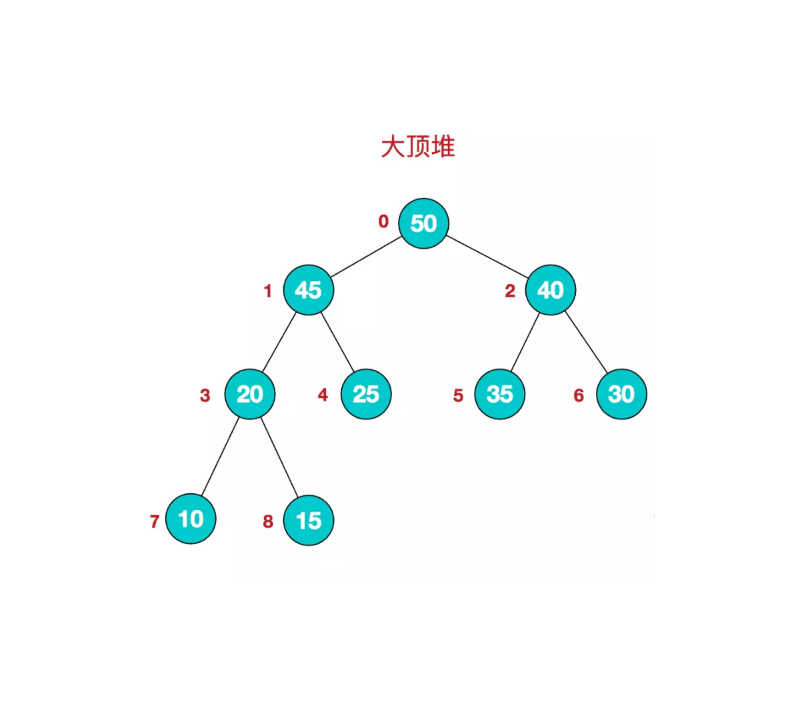
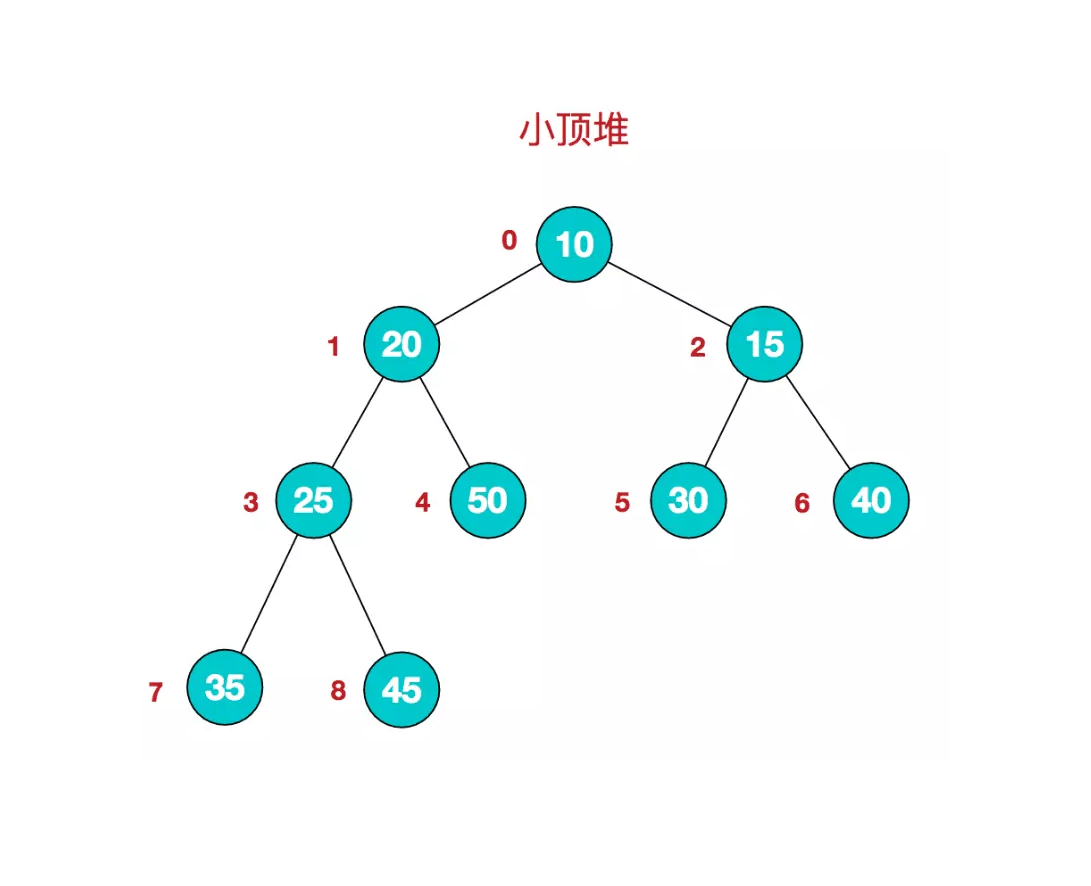
简单用公式描述一下就是：

大顶堆： arr[i] >= arr[2i+1] && arr[i] >= arr[2i+2]

小顶堆： arr[i] <= arr[2i+1] && arr[i] <= arr[2i+2]

问题二：什么是完全二叉树？

百度百科:

一棵深度为k的有n个结点的二叉树，对树中的结点按从上至下、从左到右的顺序进行编号，如果编号为i（1≤i≤n）的结点与满二叉树中编号为i的结点在二叉树中的位置相同，则这棵二叉树称为完全二叉树。

2.堆排序

百度百科:

堆排序（英语：Heapsort）是指利用堆这种数据结构所设计的一种排序算法。堆是一个近似完全二叉树的结构，并同时满足堆积的性质：即子结点的键值或索引总是小于（或者大于）它的父节点。

堆排序是利用这种数据结构而设计的一种排序算法，堆排序是一种，它的最坏，最好，平均均为O(nlogn)，它也是。

3.原理

堆排序的基本思想是：将待排序序列构造成一个大顶堆，此时，整个序列的最大值就是堆顶的根节点。将其与末尾元素进行交换，此时末尾就为最大值。然后将剩余n-1个元素重新构造成一个堆，这样会得到n个元素的次小值。如此反复执行，便能得到一个有序序列了

a.假设给定无序序列结构如下 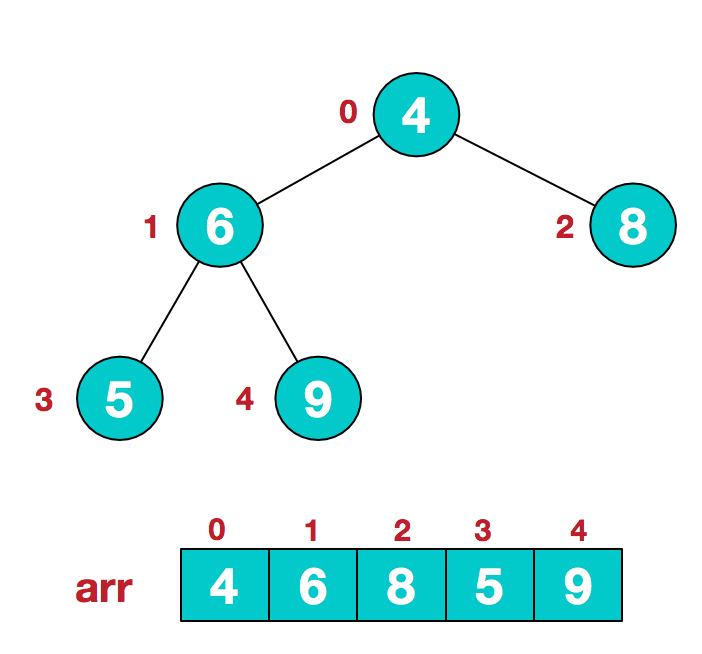　　 　　 　　 　　b.此时我们从最后一个非叶子结点开始（叶结点自然不用调整，第一个非叶子结点 arr.length/2-1=5/2-1=1，也就是下面的6结点），从左至右，从下至上进行调整。 　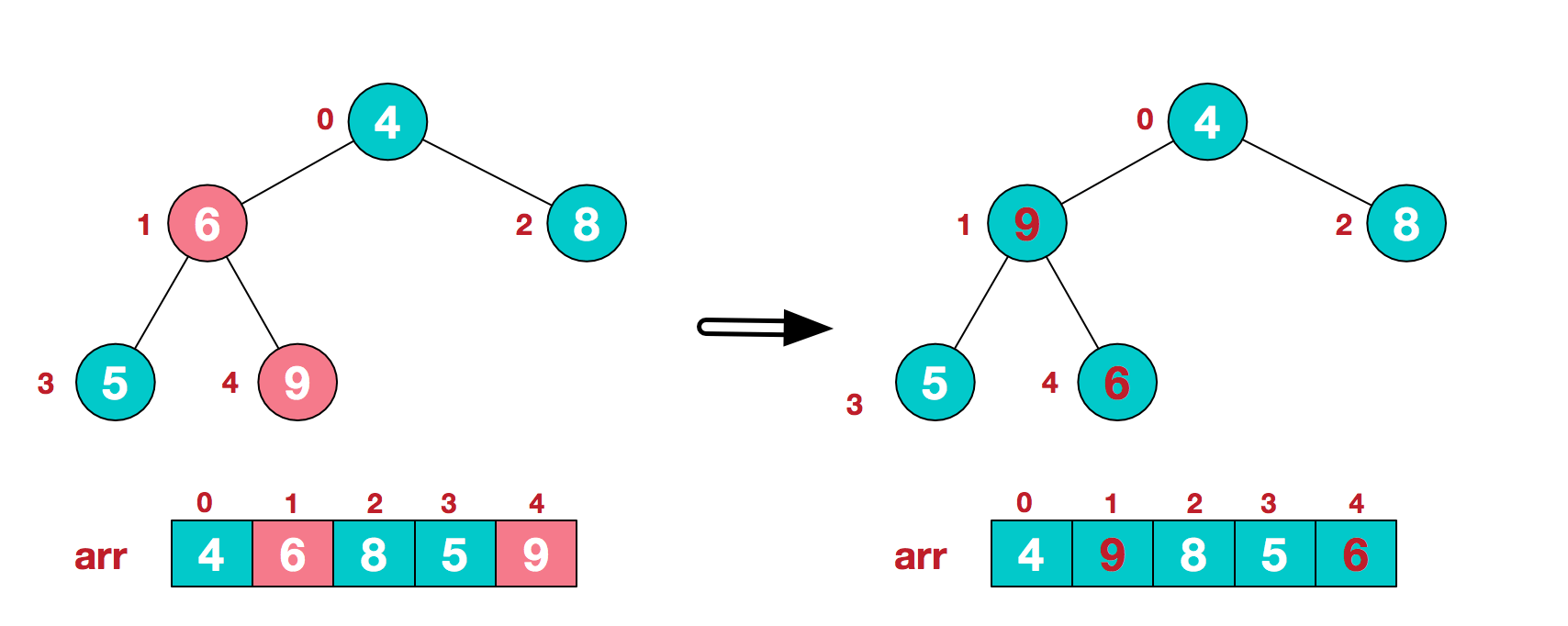　 　　 　　 　　c.找到第二个非叶节点4，由于[4,9,8]中9元素最大，4和9交换。 　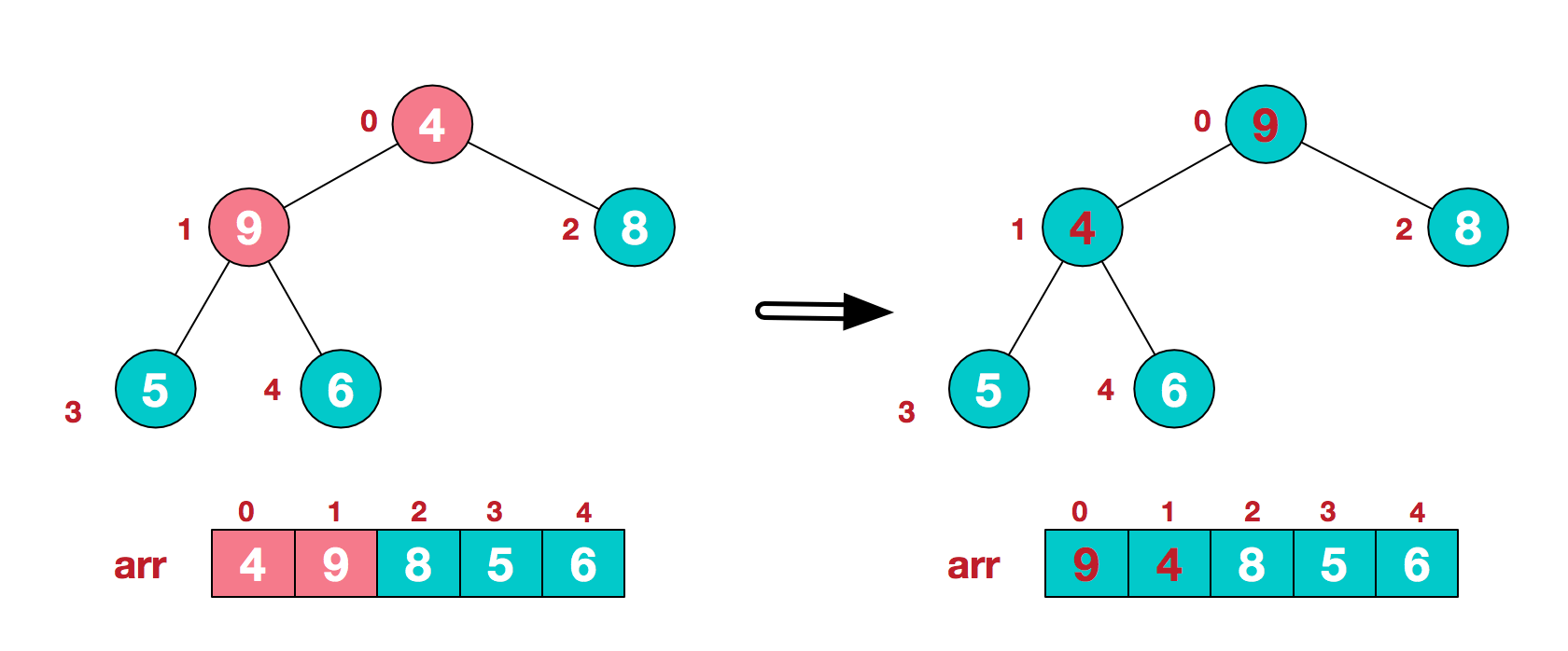　 　　 　　 　　d.这时，交换导致了子根[4,5,6]结构混乱，继续调整，[4,5,6]中6最大，交换4和6。 　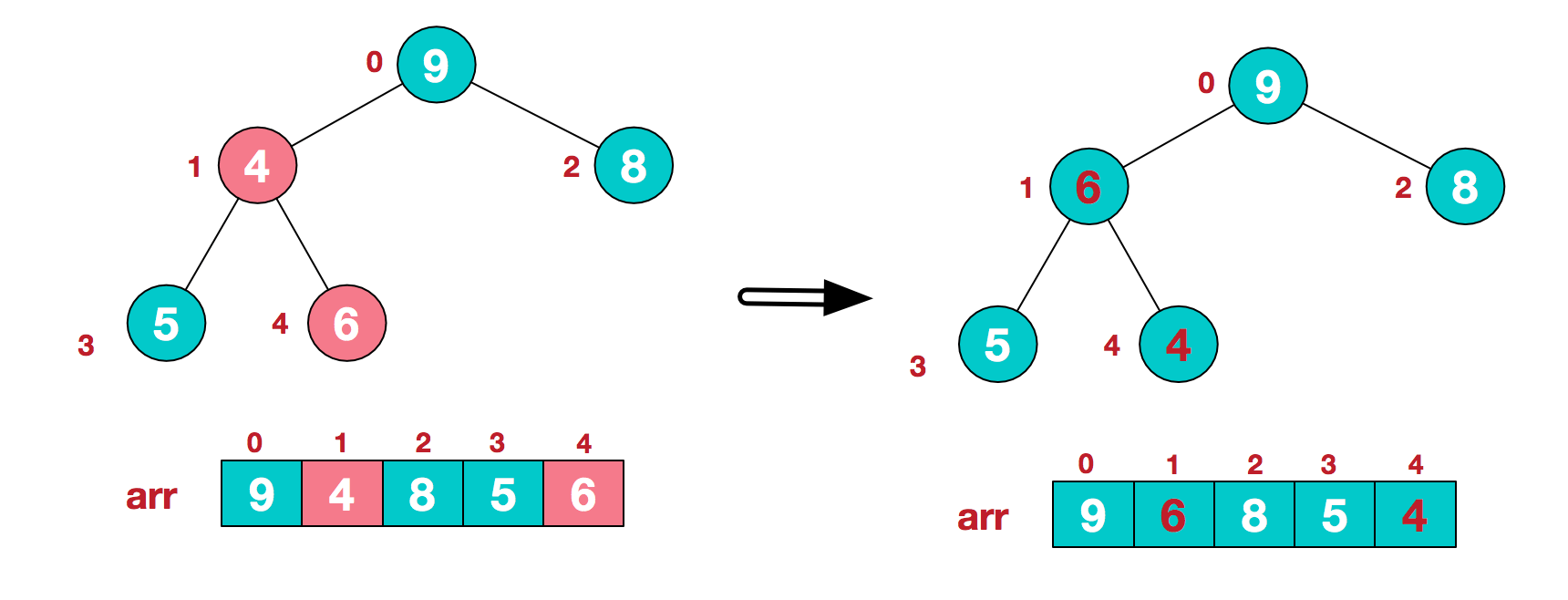　 　　 　　 　　此时，就将一个无需序列构造成了一个大顶堆。

a.将堆顶元素9和末尾元素4进行交。 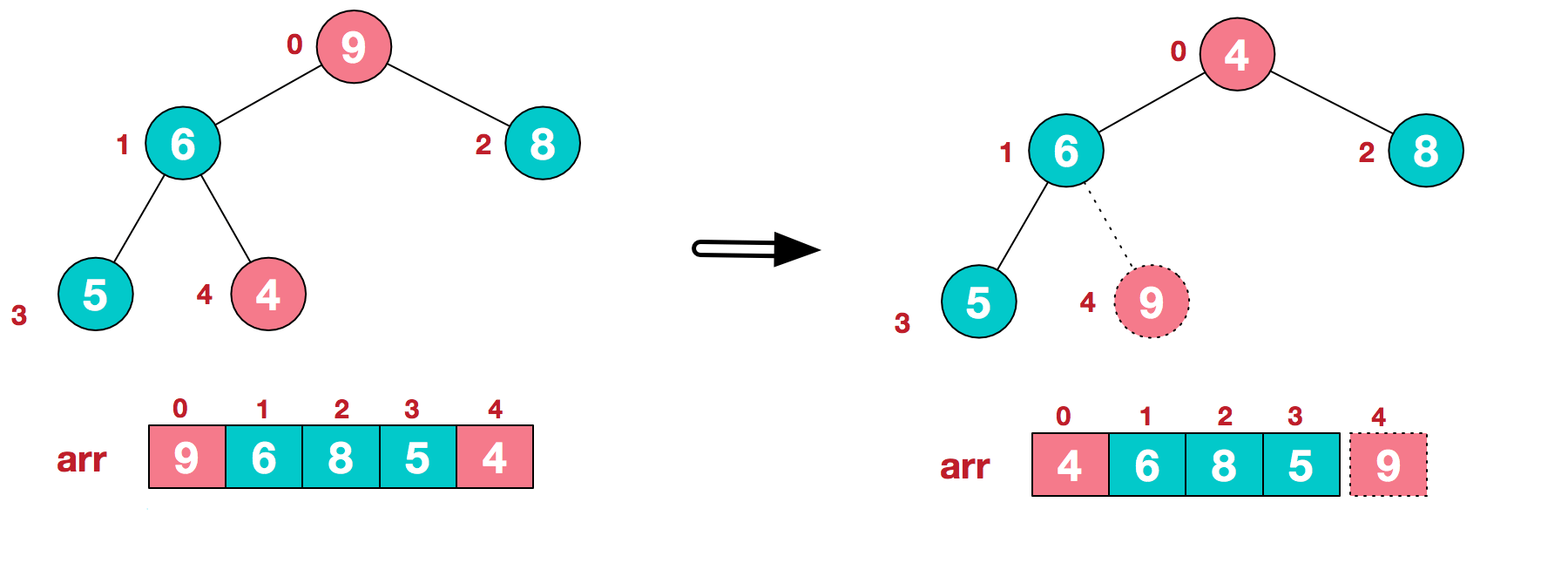　　 　　 　　 　　b.重新调整结构，使其继续满足堆定义。 　　 　　 　　 　　c.再将堆顶元素8与末尾元素5进行交换，得到第二大元素8。 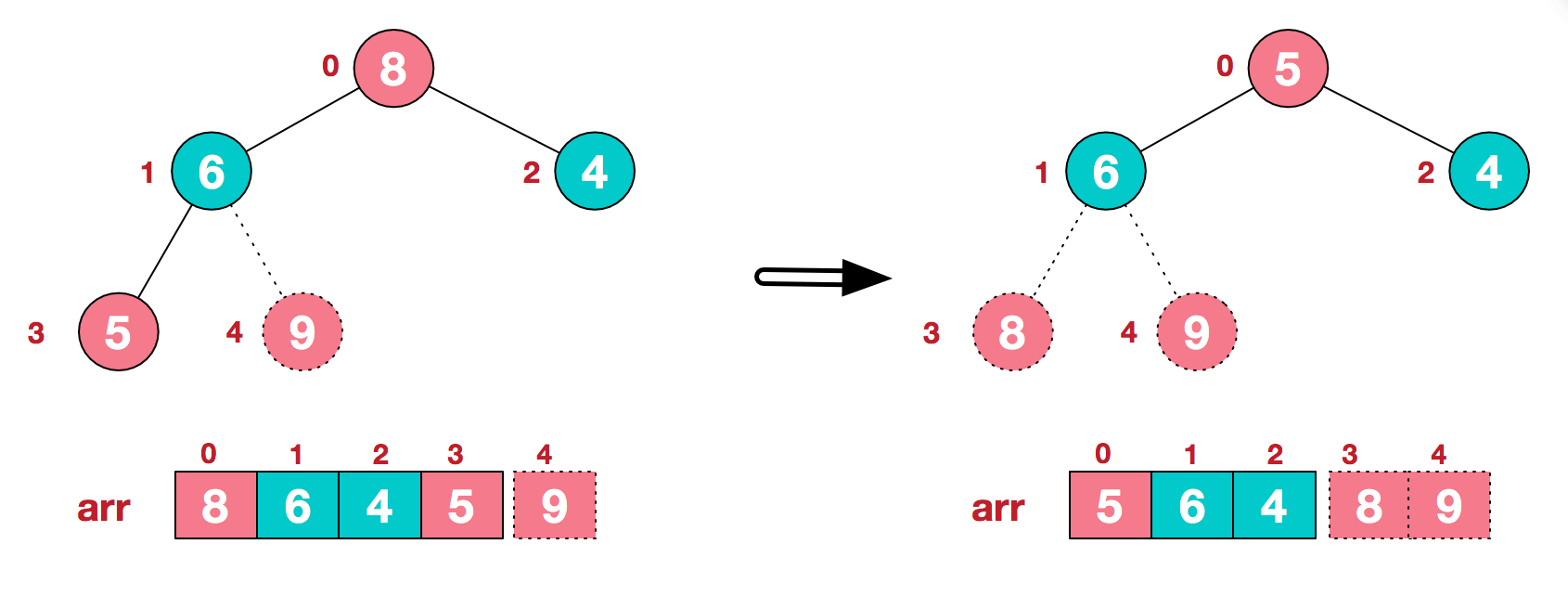　　 　　 　　 　　后续过程，继续进行调整，交换，如此反复进行，最终使得整个序列有序。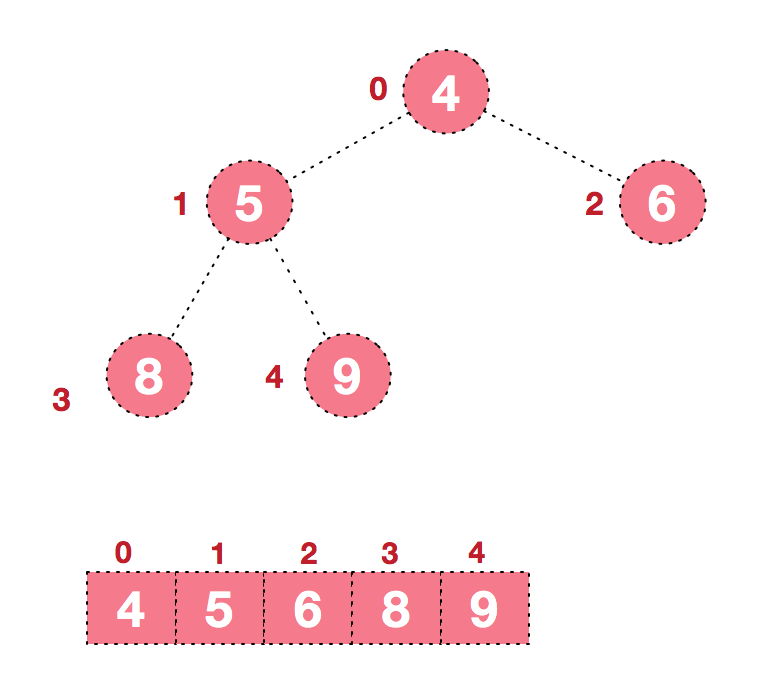 　　 　　

-　　再简单总结下堆排序的基本思路：

4.代码

代码是基于 Java语言。

package cn.javapub;

import java.util.Arrays;

public class HeapSort {

    public int[] sort(int[] sourceArray) throws Exception {
        // 对 arr 进行拷贝，不改变参数内容
        int[] arr = Arrays.copyOf(sourceArray, sourceArray.length);

        int len = arr.length;

        //构建大顶堆
        buildMaxHeap(arr, len);

        //调整堆结构+交换堆顶元素与末尾元素
        for (int i = len - 1; i > 0; i--) {
            swap(arr, 0, i);//将堆顶元素与末尾元素进行交换
            len--;
            heapify(arr, 0, len);//重新对堆进行调整
        }
        return arr;
    }

    private void buildMaxHeap(int[] arr, int len) {
        for (int i = (int) Math.floor(len / 2); i >= 0; i--) {
            //从第一个非叶子结点从下至上，从右至左调整结构
            heapify(arr, i, len);
        }
    }

    //调整大顶堆
    private void heapify(int[] arr, int i, int len) {
        int left = 2 * i + 1;
        int right = 2 * i + 2;
        int largest = i;

        if (left < len && arr[left] > arr[largest]) {
            largest = left;
        }

        if (right < len && arr[right] > arr[largest]) {
            largest = right;
        }

        if (largest != i) {
            swap(arr, i, largest);
            heapify(arr, largest, len);
        }
    }
    
    //交换元素
    private void swap(int[] arr, int i, int j) {
        int temp = arr[i];
        arr[i] = arr[j];
        arr[j] = temp;
    }

    public static void main(String[] args) throws Exception {
        int[] arr = {5, 1, 4, 2, 3};
        HeapSort heapSort = new HeapSort();
        int[] sort = heapSort.sort(arr);
        System.out.println(Arrays.toString(sort));
    }

}

返回结果：

[1, 2, 3, 3, 5]

5.最后

​ 堆排序是一种选择排序，整体主要由构建初始堆+交换堆顶元素和末尾元素并重建堆两部分组成。其中构建初始堆经推导复杂度为O(n)，在交换并重建堆的过程中，需交换n-1次，而重建堆的过程中，根据完全二叉树的性质，[log2(n-1),log2(n-2)...1]逐步递减，近似为nlogn。所以堆排序时间复杂度一般认为就是O(nlogn)级。